橫力彎曲的梁橫截面上既有彎矩又有剪力，所以橫截面上既有正應力又有切應力。下面，討論幾種常見截面梁的彎曲試驗時的切應力。

矩形截面

從發生橫力彎曲的梁上截取長度為dx的微段，該段梁上沒有載荷作用，微段兩側截面上的剪力相等，但方向相反。右側截面上的彎矩相對左側截面有增量，因為彎矩不等，因而兩截面上的正應力也不相同。

對于狹長矩形截面，由于梁的側面上無切應力，根據切應力互等定理，截面上兩側邊各點處的切應力與邊界相切，即與邊界平行，梁發生對稱彎曲，對稱軸y軸上的切應力一定沿著y方向，在狹長截面上切應力沿寬度方向變化不大。

于是，關于橫截面上切應力的分布規律，作以下假設：

橫截面上各點的切應力的方向都平行于剪力;

切應力沿截面寬度均勻分布，即與中性軸平行的橫線上各點的切應力大小相等。

截面高寬比大于2的情況下，以上述假定為基礎得到的解與彈性理論的精確解相比，有足夠的精確度。

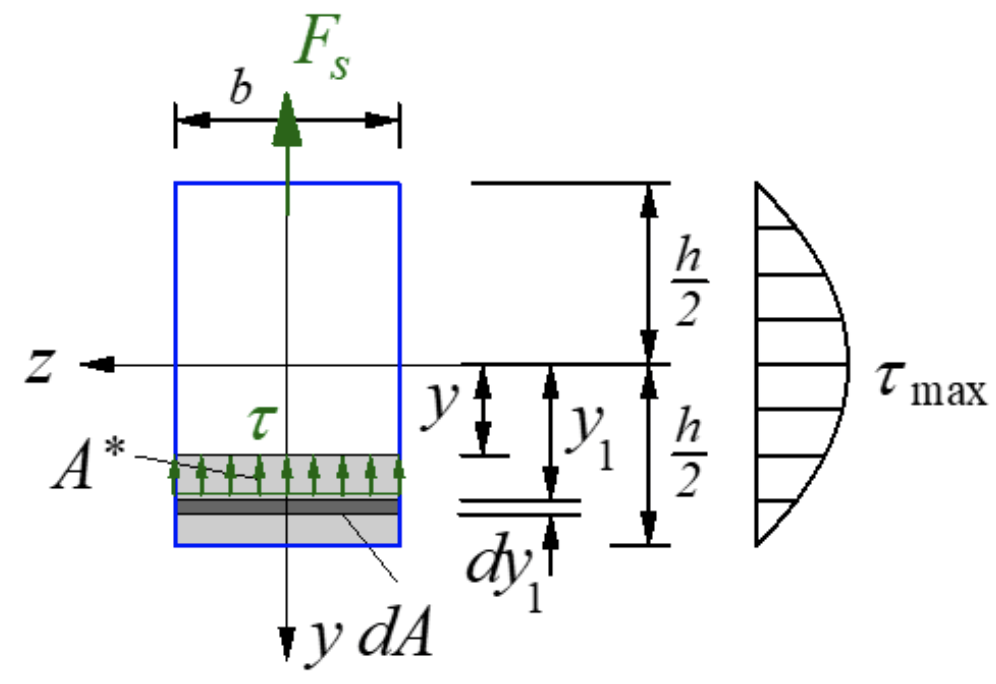
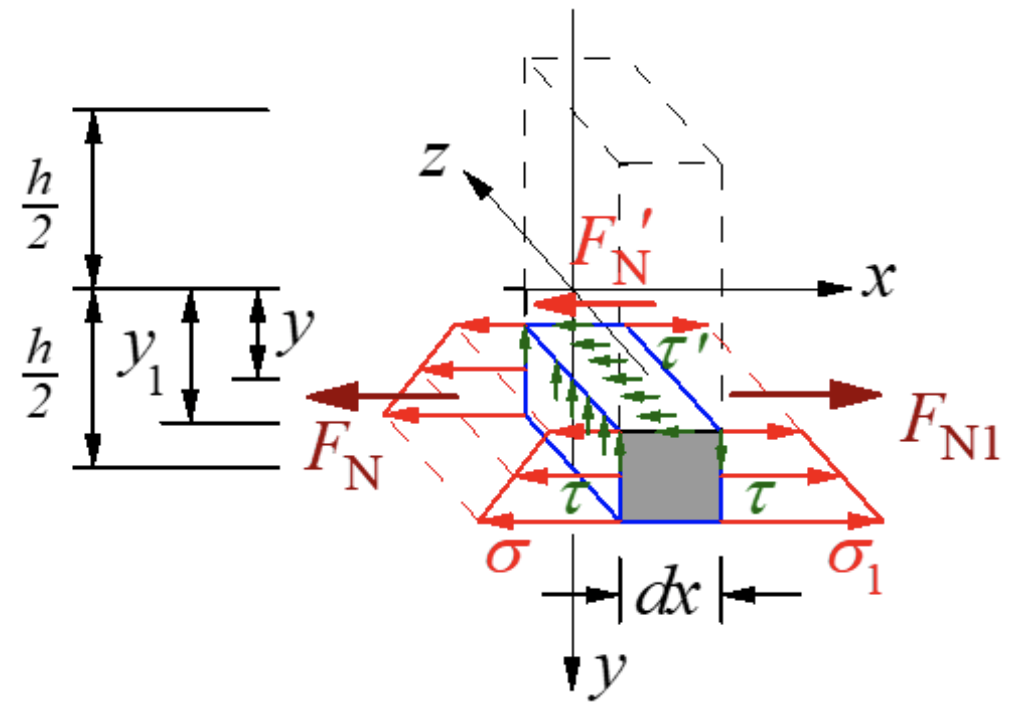
根據切應力互等定理，橫截面垂直的縱向截面上應存在與橫截面上大小相等的切應力。沿矩中性軸距離y 的縱向面把微段截開，取縱向面下側微元，受力如圖所示。

左側截面上正應力的合力為

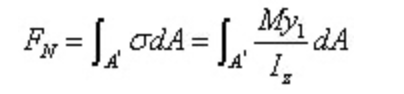
右側截面上正應力的合力為

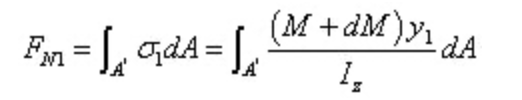
顯然這兩個合力大小不等，縱向截面上必存在一個沿軸向的力使微段保持平衡，這個力為切應力的合力，這也證明了縱向截面上存在切應力，由于dx是小量，則設縱向面的切應力均勻分布

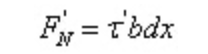
根據平衡條件

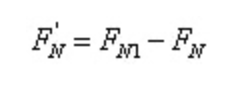
即

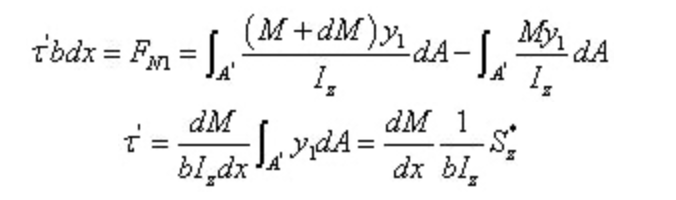
其中

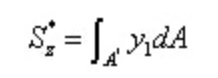
由切應力互等定理及剪力與彎矩之間的微分關系

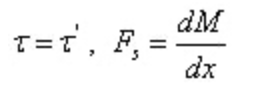
可得

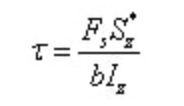
其中：b為截面上矩中性軸為y的橫線的寬度，對于矩形截面為常數;Iz為整個橫截面對中性軸的慣性矩;Sz*為橫截面上矩中性軸為y的橫線以外部分的面積對中性軸的靜矩;Fs為橫截面上的剪力。

其中

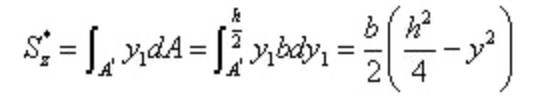
代入切應力計算公式

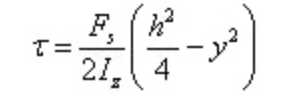
切應力沿截面高度為拋物線分布，當y=0時，即中性軸處有截面上的最大切應力

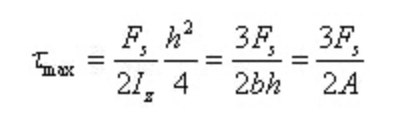
可見角應變大小沿截面高度也為拋物線分布，此時橫力彎曲時橫截面翹曲形狀如下圖，驗證了橫力彎曲變形不滿足平面假設。

剪力不變的橫力彎曲，相鄰橫截面上的切應力相同，翹曲程度也相同，縱向纖維的長度不因截面翹曲而改變，因此不會引起附加的正應力。若剪力隨截面位置而變化，相鄰兩截面上的翹曲程度不同，在截面上引起附加的正應力。

對于其他形狀的對稱截面，均可按上述的推導方法，求得切應力的近似解。對于矩形截面，在應力計算公式中截面寬度b為常數，而中性軸一側的半個橫截面面積對中性軸的靜矩最大，所以中性軸上各點處的切應力為最大。

對于其他形狀的對稱截面，橫截面上的最大切應力通常也均發生在中性軸上的各點處，只有寬度在中性軸處顯著增大的截面(如十字形截面)或某些變寬度的截面(如等腰三角形截面)等除外。因此，下面對于工字形、環形和圓形截面梁，主要討論其中性軸上各點處的最大切應力。

由切應力互等定理，在圓截面邊緣上各點處切應力的方向與圓周相切。而在對稱軸的各點處，由對稱性其切應力必沿y方向。因此，切應力分布規律可以假設為：

沿距中性軸為y 的寬度上各點處的切應力均匯交于對稱軸一點;

沿寬度各點處切應力沿y 方向的分量相等。

在提高截面的抗彎截面系數的同時，還希望用較少的材料，達到較好的經濟性。因此，一般用抗彎截面系數與截面面積的比值衡量截面設計的合理性。在相同截面面積的情況下，矩形截面(高度大于寬度)比圓形截面合理，而工字形截面或箱形截面比矩形截面合理。所以，為了充分利用材料，應盡可能地把材料放置到離中性軸較遠處。

在討論截面的合理形狀時，還應考慮到材料的特性。對抗拉和抗壓強度相同的材料(如低碳鋼)，宜采用對中性軸對稱的截面，如圓形、矩形、工字形、箱形等。這樣可使截面上、下邊緣處的最大拉應力和最大壓應力數值相等。

對抗拉和抗壓強度不相等的材料(如鑄鐵、水泥等)，宜采用中性軸偏向于受拉一側的截面形狀。

等強度梁的概念

前面討論的梁都是等截面的，抗彎截面系數為常數，但通常情況下梁的各截面彎矩是隨截面的位置而變化的。等直梁的截面設計要根據最大彎矩處進行，其最大應力接近許用應力，其余各截面上彎矩較小，應力也就較小，材料沒有充分利用。為了節約材料，減輕自重，可改變截面尺寸，使抗彎截面系數隨彎矩而變化。在彎矩較大處采用較大截面，而在彎矩較小處采用較小截面。這種截面沿軸線變化的梁，稱為變截面梁。

如變截面梁各橫截面上的最大正應力都相等，且都等于許用應力，稱為等強度梁。

以上就是江蘇容大為大家總結的彎曲試驗的切應力、梁的強度條件，如果您有更多想要了解的地方，歡迎電話咨詢：17766358885，我們會有專業的客服人員為您服務，期待您的來電！